F-statistics in population genetics
인간의 유전체는 22개의 상염색체쌍, 그리고 성염색체 2개로 구성되어있다(2n = 46). 쌍이라고 표현되는 것은 엄마-아빠로부터 물려받은 23개의 염색체가 쌍을 이뤄서 존재하기 때문이다. 23개 중 성염색체의 조합으로 우리의 성별이 결정되기도 한다.
Heterozygosity는 엄마(n_m)-아빠(n_p)로부터 각각 한 세트 받아 구성된 자손의 유전체(n_m + n_p = 2n)내에서 특정 위치에 서로 다른 allele(대립유전자)을 가지는 상태를 의미한다. 발생 과정에서 쌍커풀을 만드는데 관여하는 유전자(A)가 있는데, 그 유전자 상에 특정 위치에 변이가 포함된 경우(a) 발생 과정에서 쌍커풀이 사라지게 된다고 가정했을 때, 어떤 개체가 양 부모로부터 A, A 를 물려받은 경우 쌍커풀을 가진 아기로 태어날 것이고, a, a를 물려받은 경우 쌍커풀을 가지지 않은 아기로 태어날 것이다. 쌍커풀이 우성 형질이라고 하면, A, a를 물려받은 아기는 쌍커풀을 가지게 된다. 이 때 A, a 대립유전자를 가진 아이는 <Heterozygous하다> 라고 표현되는 Heterozygosity이고, AA, aa 유전자형을 가지는 아이는 Homozygosity이다.

*유전자형 이라는 표현을 사용했는데, 유전자형을 구성하는 염색체 쌍 내 개별 유전자를 allele, 대립유전자 라고 했으면, 대립유전자의 조합은 genotype, 유전자형 이라고 표현한다. 그리고 유전자와 여타 환경변수 등의 영향을 받아 결정되는(본 예시에서는 유전자의 영향만 있었지만) 실제 생물체에서 관찰되는 형질(예시에서는 쌍커풀의 유무)을 phenotype 이라고 한다.
그런데 이러한 Heterozygosity라는 개념은 집단유전학에서 집단 수준으로 확대된다. 당장 위에서 살펴본 가상의 쌍커풀 유전자 예시에서는 한 individual(개인, 개체)수준에서의 특정 타겟 유전자 위치의 대립유전자가 같은지, 다른지 만을 살펴봤다면, 집단 수준으로 확장된 Heterozygosity는 집단 내 개체 중 Heterozygosity인 개체의 비율을 의미한다.

어떤 집단 내에서 10명의 표본을 뽑아 유전자 확인을 해 보았다. 이 집단에서 절반은 쌍커풀을 가지고 있었고, 절반은 그렇지 않았는데 유전자 검사를 해 보니 4개 개체가 Heterozygosity인 것을 확인할 수 있었다. 그리고 그 집단 내에서 A와, a 대립유전자의 빈도를 각각 구할 수 있었다.

이 집단에서 관찰된 Heterozygosity는 10개 개체 중 Heterozygosity가 4개 개체 있었으므로 0.4로 얻을 수 있었고, 계산해둔 대립유전자 빈도를 활용해 집단의 기대 Heterozygosity는 0.42라고 계산할 수 있었다.
F-statistic은 <statistically expected level of heterozygosity in a population, wiki> 정도로 정의된다. 조금 더 엄밀하게 말하자면 <Hardy-Weinberg expectation에 비해 얼마나 heterozygosity의 감소 혹은 증가가 기대되는지>라고 할 수 있다(Hardy-Weinberg:하디바인베르크법칙, 위에서 계산한 expected Heterozygosity가 하디바인베르크 법칙을 가정한 식으로부터 계산된 것~멘델집단가정). 집단의 구조를 어떤 수준에서 보는지에 따라 Fst, Fit, Fis 로 구분할 수 있는데. 본문에서는 Fst와 Fit만 다루려고 한다. Fst, Fit 에서 S는 subpopulation, I 는 individual, T는 total population을 의미한다. 바로 직전에 계산한 heterozygosity individual count를 가지고 구한 Ho와 전체 population의 기대 heterozygosity를 이용해 Fit 를 계산할 수 있다.
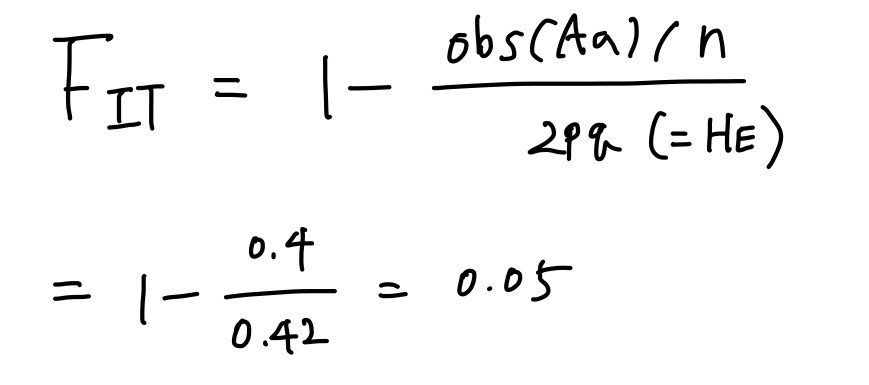
위와 같이 계산한 Fit index는 population 내에서 individual level 에서 관찰한 집단의 heterozygosity가 Hardy-Weinberg expectation에 비해 Heterozygosity가 5%정도 감소하는 것을 의미한다.
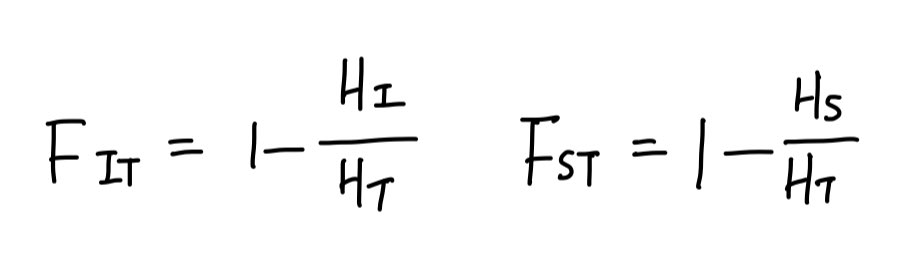
Fit가 Total population에 대한 individual level 에서의 heterozygosity를 의미한다면 Total population에 대한 subpopulation structure level에서의 heterozygosity를 마찬가지로 위와 같이 표현할 수 있는데, 이는 다음과 같은 식으로 재정의할 수 있다.
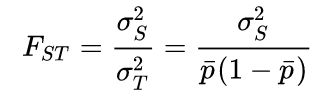
분모는 이전과 같이 total population에서의 expected heterozygosity / 2 (2pq -> pq 이므로)인데, 분자가 subpopulation의 분산으로 되어있다. Subpopulation에서의 heterozygosity는 subpopulation 내에서의 allele frequency가 새로 계산되므로, 개별 subpopulation에서의 allele frequency를 활용해서 계산된 expected heterozygosity의 summation 을 subpopulation 갯수로 나눈 값이 된다. 글로 설명하기 조금 어려운 감이 있는데 정리하면 아래와 같다.

정리가 된 건지 모르겠는데 (지금 당장은) 이 이상 들여다보고싶지 않다.. 아무튼 식을 근사해서 subpopulation의 특정 allele frequency의 분산을 분자로 사용하게 되었다는 말... (이럴거면 왜 쓰는거야...)
그래서 이 값은 Total population 내 여러 subpopulation의 유전적 조성이 얼마나 서로 유사한지, 혹은 서로 다른지를 판단하는데 활용될 수 있다.
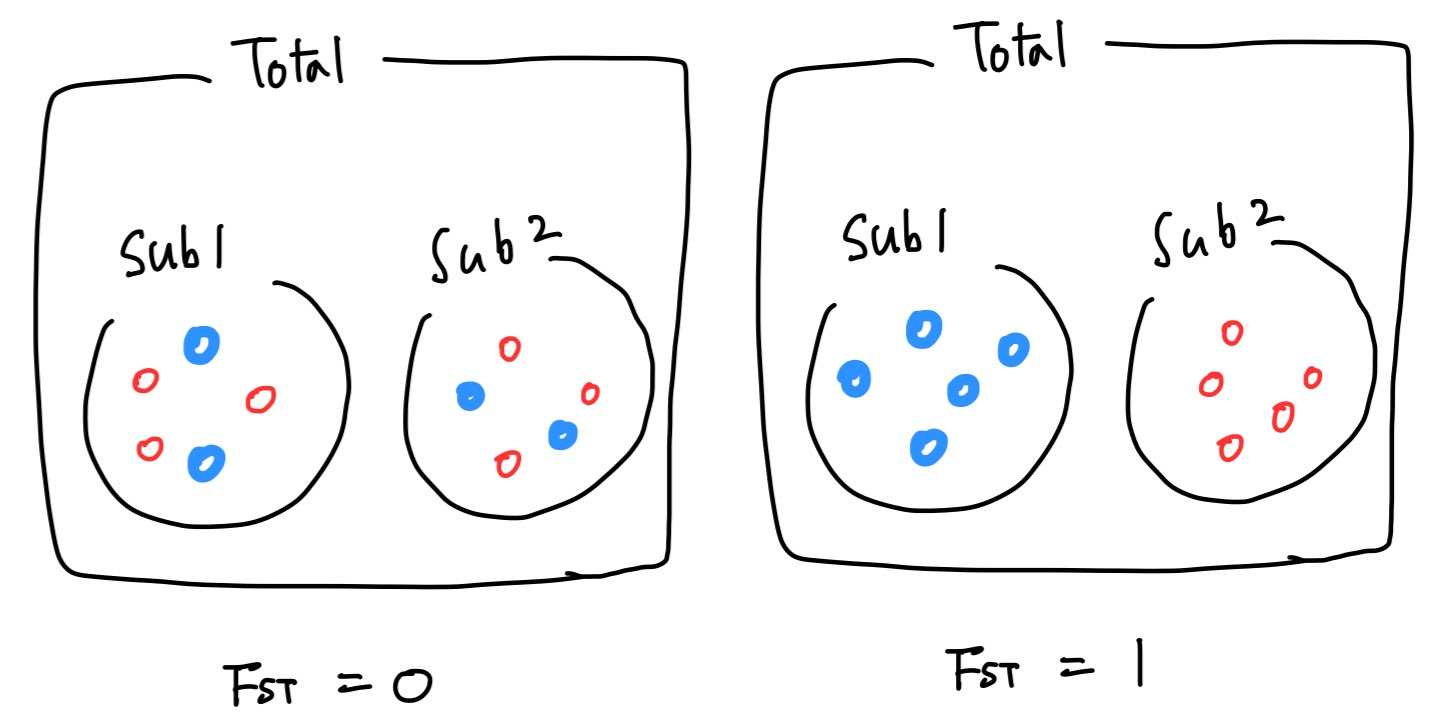
Fst값이 1에 가까울수록 subpopulation 내에서의 variation은 없고 subpopulation 사이의 variation은 크다. 반대로 Fst값이 0에 가까울수록 subpopulation 내에서의 variation은 커지고, subpopulation 사이의 variation은 작아진다. 위에서 Heterozygosity라고 표현한 것을 아래와 같이 표현할 수도 있다.

위에서 가상의 유전자를 들어 설명하긴 했으나, 유전체 내 특정한 지역, 혹은 position에 대해 계산될 수 있는 값으로 다양한 genomic element/variant를 대상으로 계산될 수 있다.

위 논문에서는 두 개 오리 품종을 각각 subpopulation으로 두고 5k genome region 내 SNP의 Fst 값을 평균내서 (a)와 같은 manhattan plot을 얻었고, 특이적으로 높은 값의 FST를 보이는 지역을 찾아 추후 분석의 target gene을 찾은 과정을 (b)-(c) plot을 통해 확인할 수 있다.